How To Find Axis Of Symmetry In Vertex Form

Learning Outcomes

Identify the vertex, centrality of symmetry, [latex]y[/latex]-intercept, and minimum or maximum value of a parabola from it'south graph.
Identify a quadratic role written in general and vertex form.
Given a quadratic part in full general form, observe the vertex.
Ascertain the domain and range of a quadratic role by identifying the vertex equally a maximum or minimum.

The graph of a quadratic function is a U-shaped curve called a parabola. Ane important characteristic of the graph is that it has an extreme bespeak, called the vertex. If the parabola opens up, the vertex represents the everyman point on the graph, or the minimum value of the quadratic role. If the parabola opens down, the vertex represents the highest betoken on the graph, or the maximum value. In either case, the vertex is a turning bespeak on the graph. The graph is also symmetric with a vertical line fatigued through the vertex, called the axis of symmetry.

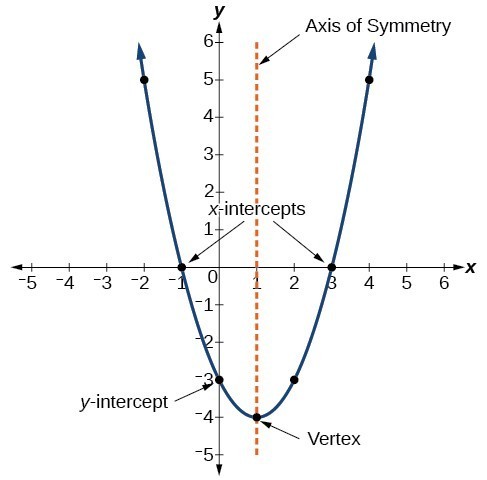
Graph of a parabola showing where the x and y intercepts, vertex, and axis of symmetry are.

The [latex]y[/latex]-intercept is the point at which the parabola crosses the [latex]y[/latex]-axis. The [latex]x[/latex]-intercepts are the points at which the parabola crosses the [latex]x[/latex]-axis. If they be, the [latex]x[/latex]-intercepts represent the zeros, or roots, of the quadratic function, the values of [latex]x[/latex] at which [latex]y=0[/latex].

Example: Identifying the Characteristics of a Parabola

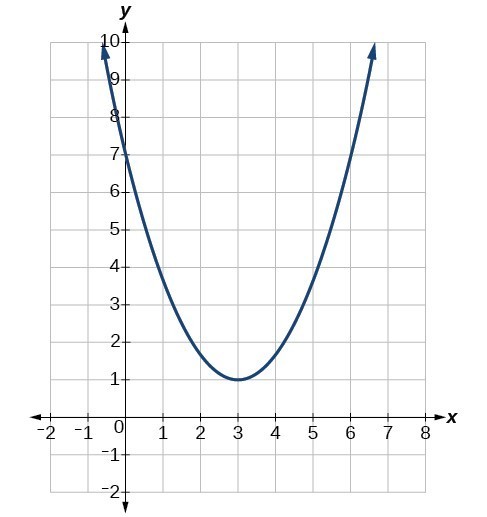
Determine the vertex, axis of symmetry, zeros, and y-intercept of the parabola shown beneath.

Graph of a parabola with a vertex at (3, 1) and a y-intercept at (0, 7).

Bear witness Solution

The vertex is the turning signal of the graph. We tin can run into that the vertex is at [latex](3,1)[/latex]. The axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is [latex]x=3[/latex]. This parabola does not cross the [latex]ten[/latex]-axis, and so it has no zeros. It crosses the [latex]y[/latex]-axis at (0, 7) so this is the [latex]y[/latex]-intercept.

Equations of Quadratic Functions

The general form of a quadratic function presents the function in the grade

[latex]f\left(x\right)=a{x}^{two}+bx+c[/latex]

where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers and [latex]a\ne 0[/latex]. If [latex]a>0[/latex], the parabola opens upward. If [latex]a<0[/latex], the parabola opens downward. We can apply the full general form of a parabola to detect the equation for the axis of symmetry.

The axis of symmetry is defined by [latex]x=-\dfrac{b}{2a}[/latex]. If we employ the quadratic formula, [latex]x=\dfrac{-b\pm \sqrt{{b}^{ii}-4ac}}{2a}[/latex], to solve [latex]a{x}^{2}+bx+c=0[/latex] for the [latex]x[/latex]-intercepts, or zeros, we notice the value of [latex]x[/latex] halfway between them is always [latex]x=-\dfrac{b}{2a}[/latex], the equation for the axis of symmetry.

The figure below shows the graph of the quadratic part written in general class as [latex]y={x}^{2}+4x+3[/latex]. In this form, [latex]a=1,\text{ }b=4[/latex], and [latex]c=3[/latex]. Because [latex]a>0[/latex], the parabola opens upwardly. The axis of symmetry is [latex]x=-\dfrac{4}{2\left(1\right)}=-two[/latex]. This too makes sense because we can see from the graph that the vertical line [latex]x=-2[/latex] divides the graph in half. The vertex e'er occurs forth the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this case, [latex]\left(-2,-i\right)[/latex]. The [latex]10[/latex]-intercepts, those points where the parabola crosses the [latex]x[/latex]-centrality, occur at [latex]\left(-3,0\correct)[/latex] and [latex]\left(-1,0\right)[/latex].

Graph of a parabola showing where the x and y intercepts, vertex, and axis of symmetry are for the function y=x^2+4x+3.

The standard course of a quadratic function presents the function in the grade

[latex]f\left(10\right)=a{\left(x-h\correct)}^{2}+k[/latex]

where [latex]\left(h,\text{ }k\right)[/latex] is the vertex. Because the vertex appears in the standard form of the quadratic function, this grade is too known as the vertex course of a quadratic function.

Given a quadratic function in full general form, observe the vertex of the parabola.

One reason we may desire to place the vertex of the parabola is that this point volition inform the states where the maximum or minimum value of the output occurs, [latex]k[/latex], and where information technology occurs, [latex]h[/latex]. If we are given the general form of a quadratic function:

[latex]f(ten)=ax^2+bx+c[/latex]

We can ascertain the vertex, [latex](h,k)[/latex], by doing the following:

Place [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex].
Find [latex]h[/latex], the [latex]x[/latex]-coordinate of the vertex, by substituting [latex]a[/latex] and [latex]b[/latex] into [latex]h=-\dfrac{b}{2a}[/latex].
Find [latex]k[/latex], the [latex]y[/latex]-coordinate of the vertex, past evaluating [latex]yard=f\left(h\correct)=f\left(-\dfrac{b}{2a}\right)[/latex]

Example: Finding the Vertex of a Quadratic Office

Find the vertex of the quadratic function [latex]f\left(ten\right)=2{x}^{ii}-6x+7[/latex]. Rewrite the quadratic in standard form (vertex course).

Try It

Given the equation [latex]g\left(x\correct)=thirteen+{x}^{2}-6x[/latex], write the equation in general form and so in standard grade.

Evidence Solution

[latex]g\left(x\right)={x}^{2}-6x+13[/latex] in general form; [latex]g\left(10\right)={\left(x - 3\right)}^{ii}+4[/latex] in standard form

Finding the Domain and Range of a Quadratic Part

Whatsoever number can exist the input value of a quadratic part. Therefore the domain of any quadratic role is all real numbers. Because parabolas have a maximum or a minimum at the vertex, the range is restricted. Since the vertex of a parabola volition be either a maximum or a minimum, the range will consist of all [latex]y[/latex]-values greater than or equal to the [latex]y[/latex]-coordinate of the vertex or less than or equal to the [latex]y[/latex]-coordinate at the turning point, depending on whether the parabola opens upwardly or down.

A Full general Note: Domain and Range of a Quadratic Function

The domain of whatsoever quadratic function is all existent numbers.

The range of a quadratic function written in full general form [latex]f\left(x\correct)=a{10}^{2}+bx+c[/latex] with a positive [latex]a[/latex] value is [latex]f\left(x\correct)\ge f\left(-\frac{b}{2a}\right)[/latex], or [latex]\left[f\left(-\frac{b}{2a}\right),\infty \right)[/latex]; the range of a quadratic office written in general class with a negative [latex]a[/latex] value is [latex]f\left(x\right)\le f\left(-\frac{b}{2a}\right)[/latex], or [latex]\left(-\infty ,f\left(-\frac{b}{2a}\right)\right][/latex].

The range of a quadratic function written in standard course [latex]f\left(x\right)=a{\left(x-h\right)}^{two}+yard[/latex] with a positive [latex]a[/latex] value is [latex]f\left(ten\right)\ge m[/latex]; the range of a quadratic office written in standard form with a negative [latex]a[/latex] value is [latex]f\left(x\right)\le k[/latex].

How To: Given a quadratic function, detect the domain and range.

The domain of whatever quadratic function every bit all real numbers.
Determine whether [latex]a[/latex] is positive or negative. If [latex]a[/latex] is positive, the parabola has a minimum. If [latex]a[/latex] is negative, the parabola has a maximum.
Make up one's mind the maximum or minimum value of the parabola, [latex]k[/latex].
If the parabola has a minimum, the range is given by [latex]f\left(ten\right)\ge k[/latex], or [latex]\left[k,\infty \right)[/latex]. If the parabola has a maximum, the range is given by [latex]f\left(x\right)\le chiliad[/latex], or [latex]\left(-\infty ,k\correct][/latex].

Example: Finding the Domain and Range of a Quadratic Function

Find the domain and range of [latex]f\left(10\right)=-5{10}^{two}+9x - 1[/latex].

Try It

Find the domain and range of [latex]f\left(x\correct)=2{\left(x-\dfrac{4}{vii}\right)}^{2}+\dfrac{8}{11}[/latex].

Show Solution

The domain is all real numbers. The range is [latex]f\left(x\right)\ge \dfrac{8}{eleven}[/latex], or [latex]\left[\dfrac{8}{11},\infty \right)[/latex].